Le signal sinusoidal
Equation de la sinusoide reelle : $$x[n]=Acos(\omega n T + \varphi)=Acos(2\pi f n T + \varphi)$$
On reconnait de suite la sinusoide reelle car le $x$ est sans barre. S'il avait ete question de sinusoide complexe, nous aurions eu un $\bar{x}[n]$.
Ou :
- $x$ : array de valeurs reelles
- $A$ : amplitude
- $\omega$ : frequence angulaire en radians
- $f=\frac{\omega}{2\pi}$ : frequence en Hertz
- $\varphi$ : phase initiale en radians
- $n$ : index de temps
- $T=\frac{1}{f_s}$ : periode d'echantillonnage en 1 seconde avec : $$t = nT$$ $$T = \frac{t}{n}$$ $$n = \frac{t}{T}$$ $$t = \frac{n}{f_s}$$ $$nT = \frac{n}{f_s}$$ $$n = \frac{\frac{n}{f_s}}{T}$$ $$T = \frac{\frac{n}{f_s}}{n}$$
Il faut ici voir $n$ comme le numero d'echantillon et $x[n]$ sa valeur.
Cette distinction a son importance puisque :
- $n$ est une valeur sur l'axe des abscisses
- $x[n]$ est une valeur sur l'axes des ordonnees
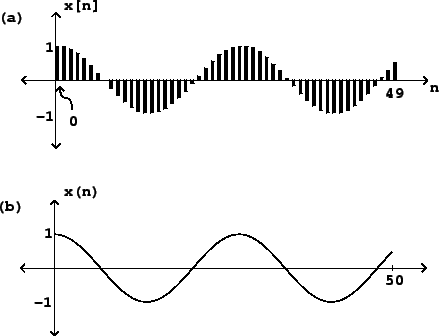
Par exemple dans le diagramme ci-dessus, on a $n=50$ mais pour autant on ignore la frequence $f$ en Hz.
Si on admettait que la valeur $n=50$ representait $1$ seconde, on pourrait dire qu'on a une frequence d'echantillonnage ($fs$) egale a $50 Hz$, soit $1$ sample toutes les $\frac{1}{50}=0.02$ seconde.
La frequence ($f$) est quant a elle egale a pratiquement $2 Hz$ car on a presque deux periodes dans ce laps de temps ($1 s$).
Si maintenant on choisissait d'appliquer une DFT sur $t=0.1$, on devrait multiplier $fs$ par $t$ pour avoir le nombre d'echantillons sur ce laps de temps. Soit $fs*t=50*0.1=5$.
Un signal sinusoidal est caracterise par son amplitude maximale et sa frequence.
Ce qui peut s'ecrire : $$g(t) = \hat G . \sin (\omega t + \varphi )$$ Avec :
- $\hat G$, : amplitude de la grandeur, appelée aussi valeur de crête.
- $\omega$, : pulsation de la grandeur en rad/s
- $(\omega t + \varphi )$, phase instantanée en radians
- $\varphi$ , phase à l'origine en radian (souvent fixée par l'expérimentateur)
Les nombres complexes
$a$ et $b$ representent les nombres reels.
$j$ est le nombre complexe et son unite imaginaire est $j=\sqrt{-1}$
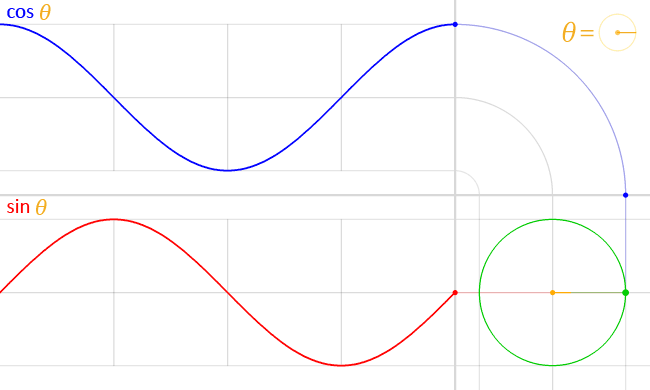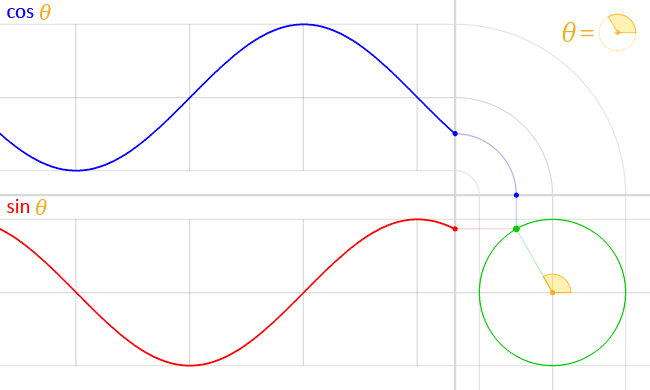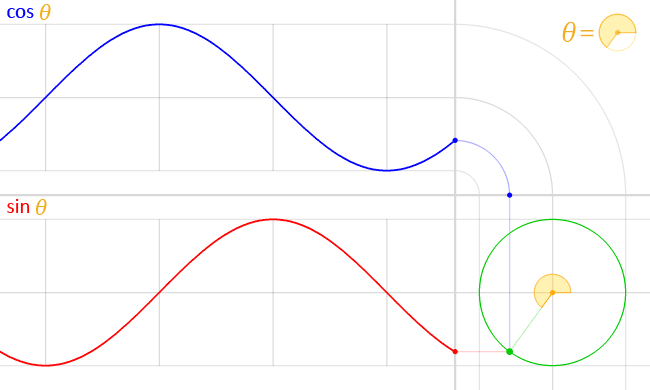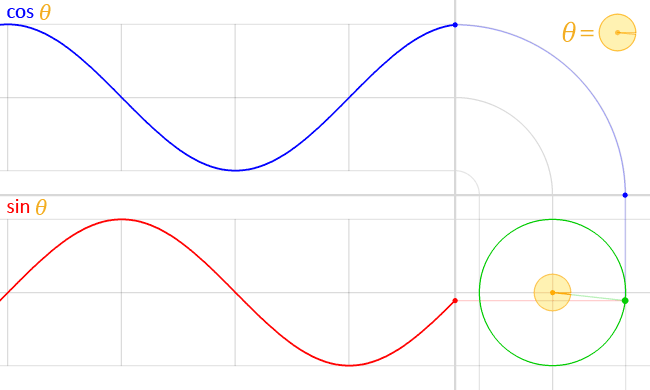
Tout ceci vient s'amuser dans ce qu'on appelle le plan complexe ou Re est l'axe des abscisses et Im l'axe des ordonnees.
Et tout autour nous avons un cercle de magnitude 1, le fameux cercle trigonometrique, appele aussi unit circle in english.
Les nombres complexes peuvent etre representes par au moins deux formes.
- rectangulaire
- polaire
La premiere represente la jonction de deux points sur l'axe du cercle et peut s'ecrire : $$(a+jb)$$
La seconde represente l'angle et la magnitude de ce point et peut s'ecrire : $$A = \sqrt{a^2+b^2}$$ $$\varphi = tan^{-1}(\frac{b}{a})$$
Avec $A$ la distance de 0 jusqu'au point et $\varphi$ l'angle de $A$ avec l'axe des Re.


La formule d'Euler
Cette formule va rassembler le cosinus et le sinus en une seule entite : $$e^{j\varphi}=cos\varphi+jsin\varphi$$
Avec : $$cos\varphi=\frac{e^{j\varphi}+e^{-j\varphi}}{2}$$ $$sin\varphi=\frac{e^{j\varphi}-e^{-j\varphi}}{2j}$$
Cette formule represente ainsi un point sur le cercle avec en abscisse $cos\varphi$ et en ordonnee $sin\varphi$
$e^{j\varphi}$ est ce qu'on appelle une complex exponential.
Le signal sinusoidal complexe
On va, ici, appliquer, a la sinusoide, la theorie des nombres complexes. $$ \bar{x}[n]= Ae^{j(\omega n T+\varphi)}= Ae^{\varphi}e^{j(\omega n T )}= Xe^{j(\omega n T)} $$
Ce que nous pouvons egalement ecrire : $$Acos(\omega n T + \varphi) + j Asin (\omega n T + \varphi)$$
Ainsi notre sinusoide reelle : $Acos(\omega n T + \varphi)$ va pouvoir etre representee avec la somme des sinusoides complexes : $$ \frac{1}{2}Xe^{j(\omega n T)}+\frac{1}{2}X^*e^{-j(\omega n T)}= \frac{1}{2}\bar{x}[n]+\frac{1}{2}\bar{x}^*[n]= \mathbb{R}\{\bar{x}[n]\} $$
Ainsi, et c'est la toute la magie de la transformee de Fourier, en ajoutant au minimum deux sinusoide complexe ensemble, nous pouvons retrouver la partie reelle de cette sinusoide.
Et il s'avere que la fonction cosinus represente la partie reelle et la fonction sinus represente la partie imaginaire : $$cos = Re$$ $$sin = Im$$
Les sequences de produits scalaires
On parle aussi de Scalar dot products of sequences.
Les y vont etre des conjugues
Donc en multipliant les deux sequences suivantes, on va obtenir un seul nombre $\langle x,y\rangle = \sum\limits_{n=0}^{N-1}x[n]*\bar{y}[n]$ $$x[n]=[0,j,1]$$ $$y[n]=[1,j,j]$$ $$\langle x,y\rangle = $$ $$0*1+j*(-j)+1*(-j)=$$ $$0+1+(-j)=$$ $$1-j$$
L'orthogonalite des sequences
x est orthogonal a y seulement si le produit scalaire de x par y est egal a 0, ce qui nous donnela formule suivante : $$x \bot y \Leftrightarrow \langle x,y \rangle=0$$
Exemple dans l'exemple suivant on a x qui est un point qui est situe au dessus de l'axe des reel et y en dessous.
x et y ont donc la meme position sur l'axe des reels (a savoir 2). sum $$x[n]=[2,2]$$ $$y[n]=[2,-2]$$ $$\langle x,y \rangle=$$ $$2*\bar{2}+2*(\bar{-2})=$$ $$4-4=$$ $$0$$
C'est ce genre d'operation basique qu'effectue la Discrete Fourier Transform.
Les fonctions paires et impaires
La convolution
En multipliant 2 sequences entre elles, on va produire une troisieme avec une forme differente.
Par exemple en multipliant une sinusoide triangulaire par une carree, cela va produire une sinusoide classique.
La formule adequate etant : $$y[n]=(x_1[n]*x_2[n])_n=\sum\limits_{m=0}^{N-1}x_1[m]x_2[n-m]$$
La serie de Fourier
Le principe est que chaque son peut etre decoupe en plusieurs ondes.
Chaque onde ayant une frequence et une amplitude differente des autres.
Ainsi chaque onde est une sinusoide (onde calculee a partir du sinus -> sin(x)).
Un son est alors la somme de toutes des sinusoides.
On peut des lors selectionne une onde dans ce son et la modifier.
Le son s'en trouve alors modifie.
Chaque onde est appele un harmonique.
L'analyse spectrale
L'analyse spectrale consiste en la decomposition d'un signal complexe en de simples parties.
Un signal complexe est donc compose de plusieurs signaux simples.
Mathematiquement on utilise l'analyse de Fourier pour analyser ces signaux.
La transformee de Fourier d'une fonction produit un spectre de frequences qui contient toutes les informations sur le signal d'origine.
On peut des lors reconstruire la fonction d'origine grace a la transformee de Fourier inverse.
C'est ce qu'on appelle en anglais "to synthetise".
D'ou le nom de synthethiseur, en francais, pour les pianos numeriques qui reproduisent (plus ou moins bien) le son des instruments correspondants.
Pour cela il est necessaire d'avoir le spectre de l'amplitude et la phase du signal de depart.
On representent generalement ces deux elements par differents moyens :
- un vecteur a 2 dimensions ;
- un nombre complexe ;
- des coordonnees polaires (de la magnitude et la phase --> phasor).
Phasor :

La transformee de Fourier
On peut etablir que l'equation suivante represente les 2 parties de la transformee de Fourier : $$ X(f)=F(x(t))=\int_{-\infty}^\infty X(t)e^{-j 2 \pi f t}dt $$
Et que la suivante definit les 2 parties de la transformee de Fourier inverse : $$ x(t)=F^{-1}\{X(f)\}=\int_{-\infty}^\infty X(f)e^{j 2 \pi f t}df $$
Le fait de parler de "2 parties" signifie que l'implementation mathematique de la transformee classique et inverse de Fourier prennent en compte tous les historiques de temps et les frequences positives et negatives du signal.
Une seule partie signifie donc que seul les temps et les frequences positives du domaine sont prises en compte.
Une paire de transformee de Fourier d'un signal represente donc les deux domaines que sont le temps et les frequences.
On peut le noter ainsi : $$ x(t) = X(f) $$
La transformee de Fourier discrete (DFT)
On parle aussi de Discrete Fourier Transform in english.
On utilise la DFT pour etablir une relation entre les echantillons du signal dans le domaine du temps et leur representation dans le domaine des frequences.
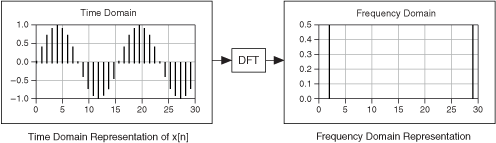
Il s'agit de la somme des samples d'un son multipliee par une complex exponential.
On peut aussi voir ca comme la totalite des points d'une sequence de valeurs reelles $x$ (un son par exemple).
Soit : $$ X[k]=\sum\limits_{n=0}^{N-1}x[n]e^{\frac{-j 2 \pi k n}{N}} = \sum\limits_{n=0}^{N-1}x[n]e^{-j \omega n} $$ $$k=0,...,N-1$$
- $N:$ number of sounds computed (la longueur de la DFT)
- $X[k]:$ spectrum
- $n:$ discrete time index (normalized time, T=1)
- $k:$ discrete frequency index
- $\omega_k= \frac{2 \pi k}{N}:$ frequency in radians
- $f_k= \frac{f_s k}{N}:$ frequency in Hz ($f_s:$ sampling rate)
Magnitude, harmonics and phase,
In a classic sound we can decompose it by its magnitude spectrum and its phase spectrum.
In the magnitude spectrum we can see the harmonics represented by peaks, composing the sound.
La magnitude d'un spectre complexe X est obtenu en prenant la valeur absolu de $|X[k]|$.
In the phase spectrum [...].
DFT: complex exponential
The input signal $x$ is multiplied by a series of complex exponentials, complex sine waves. $$\bar{S}_k= e^{\frac{-j 2 \pi k n}{N}}= cos(\frac{2\pi k n}{N})- jsin(\frac{2\pi k n}{N}) $$
If N = size of DFT; k = frequency; n = number of sine waves $$N=4$$ $$n=0,1,2,3$$ $$k=0,1,2,3$$
We have then 4 sine waves (n) of length 4 (N).
Thus we have: $$ \bar{S}_0= cos(\frac{2\pi*0*n}{4})- jsin(\frac{2\pi*0*n}{4})= [1,1,1,1] $$ $$ \bar{S}_1= cos(\frac{2\pi*1*n}{4})- jsin(\frac{2\pi*1*n}{4})= [1,-j,-1,j] $$ $$ \bar{S}_2= cos(\frac{2\pi*2*n}{4})- jsin(\frac{2\pi*2*n}{4})= [1,-1,1,-1] $$ $$ \bar{S}_3= cos(\frac{2\pi*3*n}{4})- jsin(\frac{2\pi*3*n}{4})= [1,j,-1,-j] $$
DFT: scalar product
The DFT peut egalement etre exprime avec l'equation suivante : $$ \langle x,s_k\rangle = \sum\limits_{n=0}^{N-1}x[n]\bar{s}_k[n] = \sum\limits_{n=0}^{N-1}x[n]e^{\frac{-j 2 \pi k n}{N}} $$
$e^{\frac{-j 2 \pi k n}{N}}$ est la complex exponential.
Exemple : $x[n] = [1, -1, 1, -1]$ and $N=4$
Ici $x[n]$ are 4 samples equal to 1, -1, 1 and -1.
$x[n]$ est aussi le signal d'entree (input signal).
By taking respectively: $\bar{S}_0, \bar{S}_1, \bar{S}_2, \bar{S}_3$ and multiplying by $x[n]$
Cela donne : $$\langle x,s_0\rangle = [1 * 1] + [(-1) * 1] + [1 * 1] + [(-1) * 1] = 0$$ $$\langle x,s_1\rangle = [1 * 1] + [(-1) * (-j)] + [1 * (-1)] + [(-1) * j] = 0$$ $$\langle x,s_2\rangle = [1 * 1] + [(-1) * (-1)] + [1 * 1] + [(-1) * (-1)] = 4$$ $$\langle x,s_3\rangle = [1 * 1] + [(-1) * (-j)] + [1 * (-1)] + [(-1) * j] = 0$$
$\langle x,s_0\rangle$ signifie que nous allons faire le produit de x[n] par $s_k[n]$.
Donc par exemple on va multiplier $x$ par $\bar{S}_0$, ce qui va donner : $[1,-1,1,-1]*[1,1,1,1]$.
Pareil pour $x$ par $\bar{S}_1$ : $[1,-1,1,-1]*[1,-j,-1,j]$.
Le resultat se terminant par 0 signifie que cette frequence n'est pas presente dans le signal $x$.
Donc dans les cas ou on multiplie $x$ par $\bar{s}_0$, $\bar{s}_1$, et $\bar{s}_3$ on aura un resultat signifiant que cette frequence n'est pas presente dans le signal.
Et pour $x$ multiplie par $\bar{s}_2$ on obtiendra une frequence de 4.
Ainsi donc une DFT peut etre vue comme la projection d'un signal en un ensemble de sinusoide complexe.
$N = $ nombre d'echantillons.
$k = $ nombre de periodes.
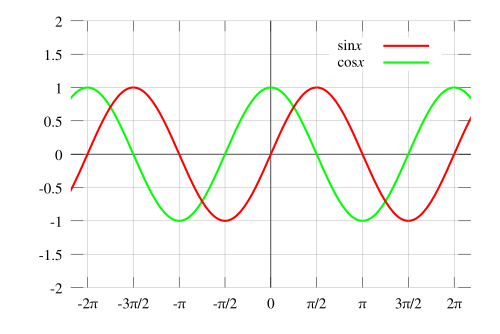
$cosine$ is an even function --> $cos(-\theta)=cos(\theta)$
$sine$ is an odd function --> $sin(-\theta)=-sin(\theta)$ $$cos(-1) = f(-1) = f(1)$$ $$sin(-1) = f(-1) = -f(1)$$
La DFT inverse
Abordons maintenant un concept assez different de la DFT mais tres ressemblant au niveau de sa formule : la DFT inverse.
Pour retrouver la partie positive de la sinusoide de base, il faut multiplier la magnitude par la partie positive de la phase.
Pour retrouver la partie negative de la sinusoide de base, il faut multiplier la magnitude par la partie negative de la phase.
$$ x[n]= \frac{1}{N}\sum\limits_{k=0}^{N-1}X[k]s_k[n]= \frac{1}{N}\sum\limits_{k=0}^{N-1}X[k]e^{\frac{j 2 \pi k n}{N}} $$
Avec $$ n=0,1,...,N-1 $$
Exemple :
Spectrum of a sequence: $ X[k]=[0,4,0,0] $ $$ N=4 $$ $$ x[0] = X*s[n=0] = (0*1) + (4*1) +(0*1) +(0*1) = 4 $$ $$ x[1] = X*s[n=1] = (0*1) + (4*j) +(0*-1) +(0*-j) = 4j $$ $$ x[2] = X*s[n=2] = (0*1) + (4*-1) +(0*1) +(0*-1) = -4 $$ $$ x[3] = X*s[n=3] = (0*1) + (4*-j) +(0*-1) +(0*j) = -4j $$
Nous faisons ici un retour en arriere puisque nous reconstruisons la sinusoide identifiee precedemment a partir des echantillons de 4 sinusoides complexes de frequences differentes.
Le resultat sera le signal complexe de depart.
Il s'agit donc de la Transformee de Fourier inverse du spectre.
Sinusoide reelle et complexe
Sinusoide reelle
Classiquement on a : $$ x[n] = acos(\omega n + \phi) $$
Egalement egal a : $$ x[n] = acos(2\pi f n + \phi) $$
On a aussi la possibilite de voir la formule suivante : $$ x[n] = Acos(2\pi f n T + \varphi) $$
With:
- $A/a = $ amplitude
- $\omega = $ l'angular frequency
- $f = $ frequency in Hz
- $n = $ time index discrete (the sample number)
- $T = $ sampling period (equals to $\frac{1}{f}$) -> how long is the period for 1 second
- $\varphi/\phi = $ l'initial phase of the sinusoid in radians --> Au sample 0, on a $n=0$
Sinusoide complexe
$$ s_k[n] = e^{\frac{j 2 \pi k n}{N}} = cos(\frac{2\pi k n}{N}) + j sin(\frac{2\pi k n}{N}) $$With:
- $k = $ number of periods
On peut egalement dire que la sinusoide complexe est egale a : $$ \bar{x}[n] = Ae^{j(\omega n T + \varphi)} = Acos(\omega n T + \varphi) + j Asin(\omega n T + \varphi) $$
Ici on a :
- $\bar{x} =$ le tableau (array) de valeurs complexes de la sinusoide
- $n =$ un entier representant l'index de temps
- $A =$ l'amplitude de la sinusoide
- $e =$ le nombre exponentiel complexe
- $\omega =$ la frequence de la sinusoide en radians (egale a $2\pi f$)
- $T =$ la periode d'echantillonnage (egale a $\frac{1}{f}$)
- $\varphi =$ la phase initiale de la sinusoide, en radians
Questions / reponses
Qu'est-ce que regroupe le traitement du signal audio (TSA) ?
C'est un domaine scientifique qui met l'accent sur les methodes de calcul pour volontairement modifier les sons.
Citez quelques applications du TSA.
Compression de donnees, synthesis, analyser le contenu d'un fichier audio.
Qu'est-ce qu'une sinusoide ?
C'est une courbe mathematique decrivant une oscillation repetitive fluide.
Qu'elles sont les deux parties d'un nombre complexe ?
La partie reelle et la partie imaginaire.
Qu'est-ce que Python ?
Un langage de haut niveau permettant de programmer une grande variete de sujets.
Qu'est-ce que SonicVisualiser ?
Un logiciel permettant de visualiser et d'analyser les sons.
Quand est-ce que deux sequences sont orthogonales ?
Quand leur produit scalaire est egal a 0.
Qu'est-ce que Numpy ?
Un package Python pour les calculs scientifiques, principalement pour les traitement d'arrays.
Quel est le signal de sortie $X[n]$ dans une equation DFT ?
Une fonction complexe representant le spectre du signal d'entree $x[n]$.
Combien d'exponentielles complexes sont calculees et utilisees dans une equation de DFT ?
Autant que le nombres d'echantillon dans le signal d'entree $x$. Ainsi la taille d'une DFT est egale a la taille du signal d'entree. Par ailleurs le nombre de sinusoides exponentielles est egale a la taille de la DFT.
Quelle serait la sortie $X[k]$ si le signal d'entree de la DFT ($x[n]$ de taille $N$) etait egale a une des exponentielles complexes ?
Une valeur de $N$ au niveau de la valeur $k$ correspondant a la frequence de l'exponentielle complexe. En effet il n'y aura qu'une seule valeur positive au niveau de la frequence, le reste etant egal a 0.
Quelle serait la sortie $X[k]$ si le signal d'entree de la DFT ($x[n]$ de taille N) etait egale a une des exponentielles complexes ?
Une fonction complexe avec des valeurs differentes de 0 pour la plupart des $k$. En effet le produit scalaire des complex exponentials qui ne sont pas celles de la DFT, donne un spectre avec des valeurs differentes de 0 pour la plupart des $k$.
Quelle serait la sortie $X[k]$ si le signal d'entree de la DFT ($x[n]$ de taille N) etait egale a une des exponentielles complexes ?
Une fonction complexe avec des valeurs differentes de 0 pour la plupart des $k$. En effet le produit scalaire des complex exponentials qui ne sont pas celles de la DFT, donne un spectre avec des valeurs differentes de 0 pour la plupart des $k$.
Quelle seront les valeurs de sortie d'un signal de sortie $X[k]$ avec un signal d'entree $x[n]$ de taille $N=8$ qui est une sinusoide reelle avec exactement 2 periodes et une amplitude de 1 ?
[0,0,4,0,0,0,4,0]
Quel son produit un diapason ?
Un son proche d'une sinusoide.
Quelle est la difference entre le spectre d'une sinusoide reelle et celui d'une sinusoide complexe, tous deux ayant la meme frequence ?
Le spectre d'une sinusoide complexe n'a qu'un seul pic, alors que celui d'une sinusoide reelle en a deux.
Sachant que la sortie d'une DFT est une fonction complexe, que peut-on mesurer depuis cette sortie ?
Les magnitudes et les phases des sinusoides presentent dans l'entree du signal.